Introducción. Los principales factores físicos de carácter climático que afectan el desarrollo y crecimiento de las plantas de cultivo son: la temperatura, la precipitación y la duración astronómica del día. De estos la temperatura está considerada como el factor que influye más trascendentalmente. Esta influencia se manifiesta en dos aspectos, uno positivo en el cual las plantas necesitan mantenerse dentro de ciertos umbrales térmicos para su buen desarrollo; y otro negativo, en el que fuera de estos umbrales, las plantas no se desarrollan correctamente e incluso pueden sufrir daños fisiológicos y morfológicos irreversibles.
Las necesidades térmicas, sin embargo, no son constantes sino que varían según la etapa vegetativa, la especie, la variedad. Por ejemplo, para los frutales caducifolios; las temperaturas invernales deben ser lo suficientemente bajas como para permitir un período de reposo que complete el ciclo vital: las yemas en letargo que deben estar expuestas a un determinado período de frío para lograr una adecuada diferenciación entre las yemas florales y las foliares y en consecuencia lograr una buena floración en la primavera. Además, las mismas bajas temperaturas favorecen la aptitud para resistir el frío.
El reposo o latencia comenzará a la caída de las hojas, es por ello que este fenómeno es propio de árboles caducifolios aunque también se habla de él para cereales de invierno. Cada especie y dentro de ella cada variedad precisa su propia acumulación de frío invernal y en cada una de éstas la acumulación de horas de frío (u horas-frío), se cuenta al comenzar la dormancia, se ha observado que en promedio las especies detienen su crecimiento a partir de los 7.2°C por lo que se ha convenido contar las horas-frío a partir de este valor (si bien con fines prácticos se toma el valor de 7°C).
Por lo que se dijo al hablar de la influencia de la temperatura, es lógico suponer que cada variedad tiene su zona geográfica óptima de cultivo, y que una variedad cumpla satisfactoriamente sus horas-frío tendrá una buena floración y si las condiciones meteorológicas y climáticas después del invierno son normales, vendrá una buena y abundante fructificación, y por tanto una buena cosecha, de tal suerte que las investigaciones acerca de este índice agroclimático son de gran utilidad en la predicción de cosechas y en general en la planeación frutícola y de cereales de invierno.
Cuantificación de horas-frío. De lo anterior se desprende la necesidad de conocer la cantidad de horas-frío que, en promedio, puede ocurrir en un cierto lugar, y de esta manera determinar:
- Si los cultivos presentes están ubicados de manera correcta en función de sus requerimientos de frío.
- Si es posible introducir nuevas especies o variedades cuyos requerimientos de frío son los que proporciona la región.
- Iniciar la colonización racional de regiones nunca dedicadas a la agricultura.
Lo más conveniente para cuantificar las horas-frío es disponer de un termógrafo y sobre las gráficas de éste contar manualmente las horas de frío que se presentan cada día. A esta forma de calcular las horas-frío se le conoce como método directo.
Pese a su grado de precisión, existen ciertas inconveniencias que le restan exactitud o limitan su uso. Entre ellas podemos mencionar:
- Como el termógrafo es un aparato graficador, su grado de exactitud no iguala al de un aparato registrador como el termómetro, de tal manera que a veces el termómetro nos indica temperaturas por debajo de los 7°C cuando el termógrafo de mínima no lo registra así y viceversa;
- la exactitud del método directo varía según se utilice un termógrafo de gráfica semanal o uno de gráfica diaria;
- al cambiarse la gráfica puede moverse la plumilla graficadora. Esto es importante, sobre todo si se tienen gráficas diarias y en cuanto a que dicho cambio se efectúa por la mañana, cuando todavía puede haber horas-frío;
- en particular para nuestro país, el más grave obstáculo para el uso del método directo no son los detalles anteriores, ni lo laborioso del cálculo, sino simplemente, la carencia de termógrafos en nuestras estaciones meteorológicas.
Este último es quizá el motivo principal por lo que se han usado los llamados métodos indirectos. Los más utilizados por su sencillez, son los de Sharpe, ideado en los Estados Unidos, y el de Da Mota, ideado en Brasil. Ambos métodos tienen como base valores calculados con el método directo, así por ejemplo, el método de Da Mota utiliza una regresión lineal entre las horas-frío encontradas por un termógrafo y la temperatura media mensual. Su fórmula es la siguiente:
H.F. = 485.1 – 28.52 X (1)
Donde:
- H.F. – horas-frío.
- X – temperatura media mensual.
- 485.1 – intercepto de la línea de regresión con el eje de las Y’s.
- -28.52 – pendiente de la línea de regresión.
En tanto que Sharpe da una tabla en la cual, para ciertos valores de la temperatura media mensual corresponde una determinada cantidad de horas-frío:
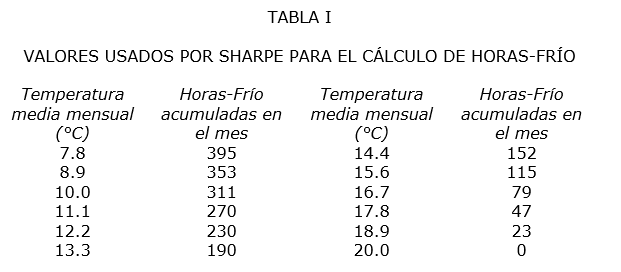
Con base en esta tabla Torres Ruiz (1983), sugiere la fórmula siguiente, obtenida por regresión lineal:
H.F. = 639 – 33TM (2)
Donde:
H.F. – horas-frío.
- T.M. – temperatura media mensual.
- 639 – intercepto de la recta de regresión con el eje de las Y’s.
- -33 – pendiente de la recta de regresión.
Una aproximación mejor obtenida con regresión lineal es la que damos a continuación elaborada en el transcurso de esta investigación por Luis Miguel Morales:
H.F. = 654.95 – 34.44 T.M. (3)
Donde:
- H.F. – horas-frío.
- T.M. – temperatura media mensual.
- 654.95 – intercepto de la recta de regresión con el eje de las Y’s.
- -33.44 – pendiente de la recta de regresión.
Esta fórmula es más aproximada a los valores dados por Sharpe que la de la formula de Torres Ruiz, citado arriba, hasta los 17°C de temperatura media mensual. Sin embargo, la representación matemática más exacta de la tabla de Sharpe, fue obtenida por Luis Miguel Morales mediante regresión polinomial:
H.F.=+ 613.02472 – 1.87018 – 6.31733 TM2 + 0.52585 TM3 – 0.02137 TM4 + 0.00036 TM5 (4)
Donde:
- H.F. – horas-frío.
- T.M. – temperatura media mensual.
Las constantes son los coeficientes de regresión para cada término de la serie.
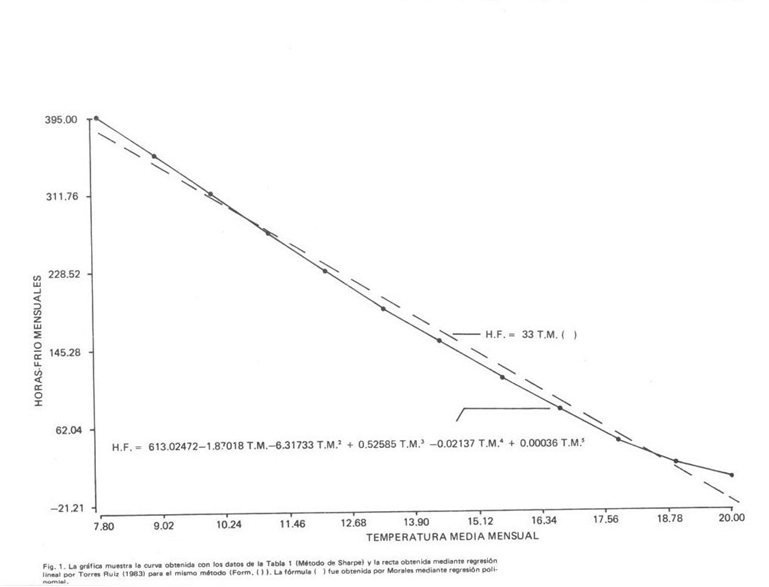
La expresión gráfica de las fórmulas (2) y (4) se observa en la figura 1, y los resultados numéricos del ajuste de las fórmulas (2), (3) y (4) para el método de Sharpe se encuentran en la tabla II. En la figura 1, la curva corresponde tanto a la representación gráfica de los datos de la tabla I como al ajuste de la fórmula (4).
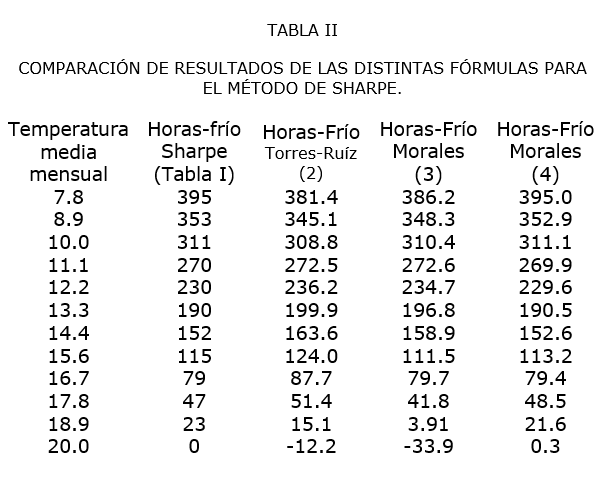
De esta tabla se observa que, efectivamente, la fórmula (4) es la más adecuada a los valores de Sharpe. Sin embargo, con fines prácticos se ha tomado la fórmula (3), ya que sus resultados son más cercanos a los de la realidad que los de la fórmula (4), como se verá más adelante.
Otros métodos son el de Weinberger y el de Crossa-Raynaud. El de Weinberger, se basa en una gráfica obtenida con las temperaturas medias de diciembre y enero. El de Crossa-Raynaud utiliza la siguiente fórmula:
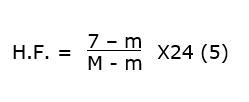
Donde:
- H.F. – horas-frío.
- M – temperatura máxima diaria.
- m – temperatura mínima diaria.
- 24 – horas del día.
- 7 – límite superior de las horas frío (en °C).
Cuando se comparan los resultados de los métodos indirectos citados (excepto Weinberger), la diferencia entre ellos suele ser hasta de un 100% (con los métodos originales) lo cual puede significar que uno de ellos es el correcto y los demás no son confiables o bien que ninguno es confiable.
Para verificar estas hipótesis se utilizó el método directo basándose en el termógrafo del Observatorio del Colegio de Geografía de la Universidad Nacional Autónoma de México. Al final del conteo de horas frío mediante el método directo se encontró que era válida la última hipótesis mencionada; el método más aproximado es el de Da Mota, seguido muy de cerca por el de Crossa-Raynaud y finalmente el de Sharpe como se apreciará más adelante.
Sin embargo, los resultados obtenidos por los métodos indirectos dejan mucho que desear, por lo que se elaboró un método indirecto que, por lo menos, para los datos del Observatorio del Colegio de Geografía, probó ser más exacto: el método Gómez-Morales.
La idea de elaborar este método surgió como consecuencia de trabajar gráficas del termógrafo: teóricamente un procedimiento que representara con aproximación la marcha diaria de la temperatura es más exacto que uno que utiliza correlaciones, como los métodos indirectos tradicionales.
Asimismo, se tomó en consideración que en las estaciones meteorológicas de México, se registran al menos tres datos diarios de temperatura: mínima, ambiente (8:00 A.M.) y máxima.
Con base en lo anterior se elaboró el método Gómez-Morales en su modalidad diaria, que simula el comportamiento de la temperatura. Obviamente esta simulación tiene algunas fallas; si se compara una gráfica trazada con los datos usados por el método con una gráfica del termógrafo para una misma fecha, se observa que las mayores diferencias se presentan durante el mediodía y tarde, mientras que en la noche y madrugada el ajuste entre ambas gráficas es más aproximado (fig. 2). Estas diferencias se explican porque generalmente durante las horas diurnas la temperatura sufre mayores oscilaciones que en la noche y en la madrugada.
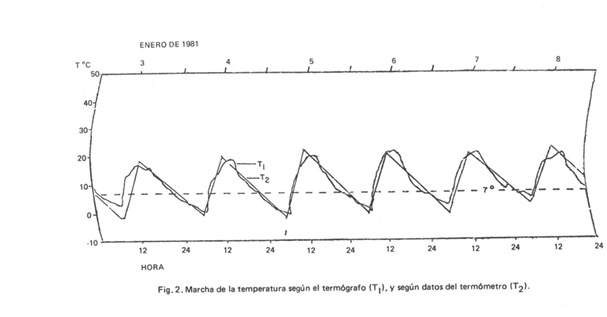
Sin embargo, como las horas frío se presentan por lo general durante la noche y primeras horas del día, se pueden hacer a un lado las deficiencias observadas en el período diurno.
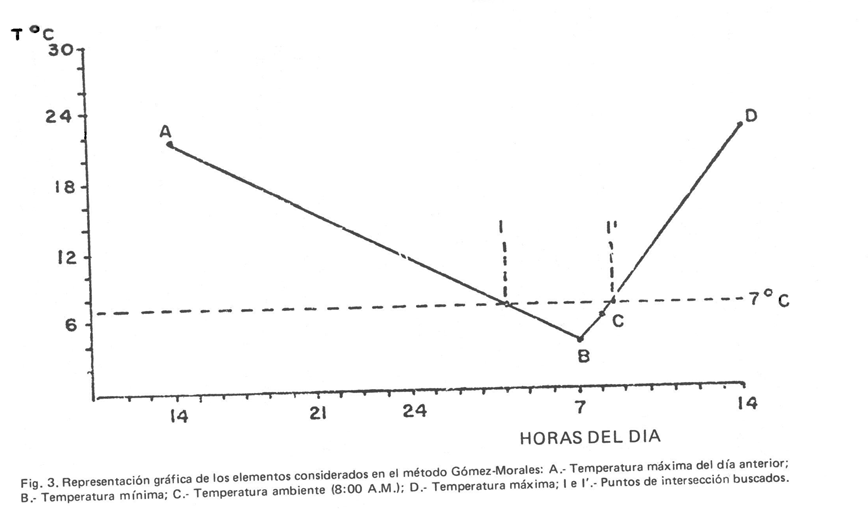
Según la representación gráfica del modelo (fig. 3), se observa que existen cuatro rectas: AB, BC, CD y la recta señalada por la línea punteada. Esta última intersecta a la recta AB en el punto I, y a la recta CD (o a la BC si es el caso) en el punto I’. El segmento de la recta definido entre los puntos I e I’ representa el lapso durante el cual la temperatura estuvo por debajo de 7°C, esto es, la cantidad de horas frío para ese día. Luego entonces, interesa encontrar los valores de las abscisas para ambos puntos de intersección y luego calcular la diferencia entre I e I’.
Simplificando el sistema de ecuaciones se obtuvo una primera fórmula:
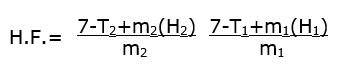
Donde:
- H.F. – horas frío.
- 7 – constante numérica (límite superior de las horas frío, en °C.
- T1 – temperatura máxima del día anterior (punto A en la gráfica).
- T2 – temperatura mínima (punto B) o temperatura ambiente (punto C)
según sea el caso.
- m1 – pendiente de la recta AB donde se encuentra la primera intercepción (punto I).
- m2 – pendiente de la recta BC o CD según sea el caso donde se encuentre la segunda intercepción (punto I’).
- H1 – hora relativa de la ocurrencia de la temperatura máxima del día anterior, se obtiene con:
H1 = HA – 24
Donde:
- HA – hora a la que ocurrió la máxima del día anterior. (Generalmente se da a las 14:00 horas por lo que H1 = 14-24=10
- H2 – hora a la que ocurrió la temperatura mínima o la ambiente, según sea el caso. (Se han tomado los valores de 7:00 horas para la mínima y de 8:00 horas para la ambiente*[1]).
Los casos que determinan los valores de T2, m2 y H2 son:
1° Si la temperatura ambiente < 7°C entonces:
T2 – temperatura ambiente.
m2 – pendiente de la recta CD
H2 – hora de ocurrencia de la temperatura ambiente.
2° Si la temperatura ambiente > 7°C entonces:
T2 – temperatura mínima.
M2 – pendiente de la recta BC
H2 – hora de ocurrencia de la temperatura ambiente.
De la fórmula anterior, por sucesivas simplificaciones algebraicas, se obtuvieron finalmente dos fórmulas, de acuerdo con los dos casos mencionados:
- Si TA es mayor a 7°C entonces:

2. Si TA es menor o igual a 7°C entonces

Donde:
- H.F. – horas-frío.
- TMA – temperatura máxima del día anterior.
- TM – temperatura máxima.
- TA – temperatura ambiente (8:00 A.M.).
- Tm – temperatura mínima.
Los valores numéricos son constantes
Las fórmulas corresponden al método en su forma diaria. Sin embargo, al estar trabajando con él surgió la idea de aplicarlo en forma mensual, es decir, trabajar con medias mensuales. Desde luego esto nos enfrentaría con el problema ya observado en los métodos originales de Da Mota y Sharpe, de que al anular las oscilaciones diarias de la temperatura, los resultados acumulados para cada mes del período otoño-invernal, son generalmente muy bajos. Sin embargo, se hicieron ajustes para eliminar o al menos disminuir este error.
Esta variante mensual del método Gómez-Morales, funciona con las fórmulas (6) y (7), únicamente varían los datos, de la siguiente forma:
- TMA – Temperatura media máxima del mes anterior
- TM – Temperatura media máxima del mes presente
- Tm – Temperatura media mínima del mes presente
- TA – Temperatura media ambiente del mes presente
Además hay que considerar el siguiente ajuste para los valores TM, Tm y TA:
- Se cuentan los días en los que hubo “frío”, esto es, los días en los que la temperatura mínima (Tm) fue menor a 7°C.
- Se obtienen las medias mensuales para todos los días del mes (medias de TMA, TM, Tm y TA).
- Se obtienen las medias mensuales para los mismos parámetros pero contando únicamente los días en los que hubo “frío”. (Si no existe “frío” para algún mes se tomarán las medias mensuales normales, por ejemplo, cuando se esta calculando para el mes de noviembre se necesita la TMA de octubre; pero como en este mes generalmente no hay frío, se toma la media máxima mensual calculada con los 31 días de octubre)
- Con los resultados obtenidos en los pasos (2) y (3) se obtienen promedios para cada parámetro, excepto para TMA.
- Seguidamente se obtiene un promedio entre los valores medios normales y los valores medios calculados con los días en que la temperatura mínima fue menor a 7°C.
- El promedio así obtenido para las máximas es el que se utiliza en las fórmulas, igualmente el calculado para las ambientes. Para las mínimas se procede como sigue:
- Llamemos: A, el promedio de las mínimas, considerando únicamente los días en que la temperatura mínima diaria es menor a 7°C; B, el promedio de las mínimas obtenido en la fórmula usual; C, el promedio de los dos valores anteriores; D, el porcentaje de días con temperatura mínima inferior a 7°C respecto al total de días del mes; luego:
E= (D x B)/100 y Tm = 4 + E
Entonces:
Si Tm es mayor que C entonces Tm = C
De lo contrario Tm=4+E
Si Tm es menor que A entonces Tm = A
De lo contrario Tm = C.
Finalizado este procedimiento se aplican las fórmulas (6) y (7).
Además de esta variante mensual se desarrolló una más, la cual utiliza las mismas fórmulas que las variantes diarias y mensual, pero con valores periódicos, es decir, tomando los valores medios de cada parámetro, contando los días de los 4 meses del período otoño-invernal. Los resultados y la descripción de esta variante no se incluye en el presente trabajo, en virtud de que se está afinando su método, aunque en principio ha dado mejores resultados que los métodos de Sharpe, Da Mota y Crossa-Raynaud.
Análisis comparativo. Para determinar qué método indirecto conviene utilizar en un estudio de planeación frutícola es menester conocer cuál es el que arroja resultados más precisos, de manera que nuestro trabajo sea lo más útil y confiable.
Los métodos:
En el presente trabajo se han tomado los métodos de Gómez-Morales, en sus modalidades diaria y mensual, el método de Crossa-Raynaud y los métodos de Da Mota y Sharpe, en su forma mensual original y también una adaptación diaria de ambos. El método de Weinberger se ha excluido, ya que únicamente considera horas-frío para los meses de diciembre y enero, mientras que el resto incluye además a noviembre y febrero.
Fórmulas:
Gómez-Morales: (diaria y mensual). Para ambas modalidades se han utilizado las fórmulas (6) y (7).
Crossa-Raynaud: se ha tomado la fórmula (5).
Da Mota: (mensual). Fórmula (1).
Da Mota: (adaptación diaria).
H.F. = 485.1 – 28.52 TM/M (8)
Donde:
T.M. = temperatura media diaria.
- = número de días del mes.
Sharpe: como los resultados de este método aplicado con las fórmulas (2), (3) y (4) son demasiado altos, se optó por dividir todas las fórmulas entre dos. De esto se obtuvo que la fórmula que dio mejores resultados fue la fórmula (3) de L. M. Morales, por lo que en este apartado se ha hecho uso de ellos.
Sharpe (mensual). Fórmula (3) (dividido entre dos)
Sharpe (adaptación diaria):
H.F. = [(654.95 – 34.44 TM)/2]/M (9)
Donde:
TM – temperatura media diaria.
M - número de días del mes.
Los datos. En este artículo se dispuso de los datos de temperatura mínima diaria, temperatura ambiente diaria (8:00 A.M.) y temperatura máxima diaria para los meses de noviembre, diciembre, enero y febrero, registrados con los termómetros de máxima y mínima del Observatorio Meteorológico del Colegio de Geografía, en la Ciudad Universitaria. Además se contó con las gráficas semanales y diarias de la temperatura, procedentes de la misma dependencia. La serie disponible consta de 20 años (1963-1983). Sin embargo, sólo se utilizaron 11 años debido a que en algunos de ellos faltan datos del termógrafo o bien del termómetro o ambos a la vez. Los años considerados son los siguientes (tomando el período de 4 meses que va desde noviembre a febrero): 1970-1971, 1971-1972, 1972-1973, 1974-1975, 1975-1976, 1977-1978, 1978- 1979, 1979-1980, 1980-1981, 1981-1982, 1982-1983.
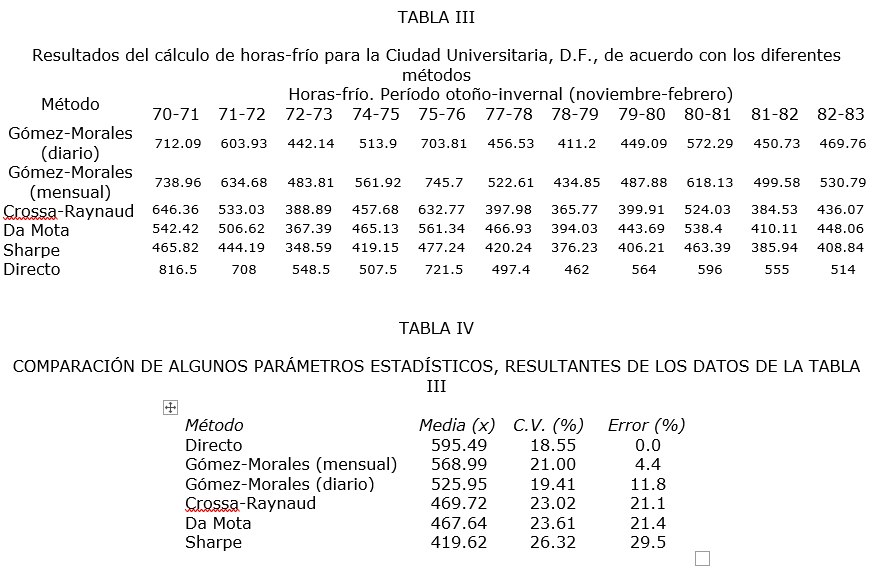
En la tabla siguiente (Tabla III), se puede apreciar el grado de precisión arrojado por los diferentes métodos de cálculo de horas-frío, tomando como referencia al método directo. Es fácilmente observable que el mejor método es el de Gómez-Morales (mensual) seguido muy de cerca por el de Gómez-Morales (diario) y con resultados más bajos encontrados a Crossa-Raynaud, Da Mota (mensual) y Sharpe (mensual).
De esta tabla se obtuvieron mediante métodos estadísticos los resultados de la Tabla IV, en la que se demuestra que los mejores métodos fueron los de Gómez-Morales en sus modalidades diaria y mensual.
En esta tabla se observa que el promedio de horas-frío, para Ciudad Universitaria es de casi 600 horas-frío según el método directo, de manera que el método que más se aproxime a este valor es más válido que el resto. La diferencia entre el resultado del método directo, tomado como referencia y los métodos indirectos considerados, está expresada como un error en la cuarta columna de la tabla. Otro parámetro que nos da idea de la bondad de cada método, es el coeficiente de variación (C.V.), el cual es resultado de dividir la desviación estándar del método directo entre la media aritmética de cada uno de los otros métodos multiplicada por cien. Así, tenemos que el método cuyo coeficiente de variación se acerque más al coeficiente de variación del método directo, será el mejor estimador de las horas-frío.
Para tener una idea más clara de la variación interanual de los métodos, se ha hecho una comparación de sus resultados diarios, misma que se muestra en la tabla V. También se han elaborado las figuras 4 y 5 para el mismo período otoño-invierno.
Respecto al período que se considera normalmente para la estimación de horas-frío, y que abarca de noviembre a febrero, los suscritos han observado que al menos en la República Mexicana el período con temperaturas por debajo de 7°C comienza usualmente en la segunda quincena de octubre y termina hasta la primera quincena de marzo, por lo que cabría replantear, el período en que se deben contabilizar las horas-frío, de tal manera que el término requerimientos de frío invernal debiera ser requerimientos de frío otoño-invernal.
Por otra parte, tomando en cuenta que el límite de la temperatura para conservar el estado de latencia, cambia según la especie y variedad, consideramos apropiado que este límite sea variable en función de la planta y no se mantenga en 7.2°C como se utiliza convencionalmente, sobre todo cuando el límite se ubica arriba de este valor, ya que hay especies que comienzan a satisfacer sus necesidades de frío, con temperaturas mayores a 7.2°C.
Otra consideración que conviene tener presente es que el requerimiento de frío en una especie y/o variedad no es un valor fijo, sino que varía según se presente el invierno. Entre las condiciones otoño-invernal que modifican las necesidades de frío están:
- Insolación intensa, ausencia de nubosidad y baja humedad relativa, que provocan fuerte oscilación diaria de la temperatura.
- Irregularidades térmicas durante el otoño-invierno (presencia de épocas definidas de gran calor).
- El comportamiento anormal del tiempo atmosférico en las estaciones otoño-invernal
De la misma manera el cambio espacial de una especie o variedad fuera de su ámbito normal de desarrollo puede ocasionar modificaciones en sus necesidades de frío otoño-invernal.
Por lo que respecta a los métodos existe la tendencia, entre algunos estudiosos de este índice, de obviar algunas cuestiones que a nuestro juicio son importantes: por ejemplo, Reyna (1983), Calderón (1983) y Muñoz Santamaría (citado por los autores anteriores) han llegado a la conclusión de que los métodos de Da Mota y Weinberger son los más apropiados para aplicarse en la República Mexicana. Basándose en la consideración de que ambos métodos “proporcionan la estimación más cercana a la realidad de efecto efectivo de frío sobre los árboles en un lugar dado … los datos obtenidos con estos métodos no necesitan en condiciones normales ser sometidos a ajustes por índices de corrección”. (Calderón, 1983).
Estos resultados consideran el total de días de los cuatro meses, es decir 121 días, pero si se cuentan únicamente los días en que según el termógrafo hubo frío, entonces se tienen los siguientes resultados finales:
Número de días con “frío”: 109
Número de días con mejor aproximación. % de confiabilidad:
Gómez-Morales 84 77.0
Crossa-Raynaud 26 23.8
Da Mota 20 18.3
Sharpe 10 9.1